Perhaps you have heard of the Feynman Sprinkler before; it’s a relatively famous physics conceit, though admittedly, physics mind-benders are not necessarily part of the public consciousness. Feynman himself was particularly coy when writing about it in his autobiography, abstaining from sharing the result of his experiment, which has led to the typical internet speculation (see: airplane on a treadmill). It’s such a neat problem because smart, informed people can come to completely different conclusions as to what happens when you run a sprinkler in reverse.
 |
|
 |
| Normal Sprinkler |
|
Feynman Sprinkler |
Obviously, our “normal” sprinkler will spin clockwise. Feynman wanted to know what direction it would spin when run in reverse. I think there’s a general consensus that an underwater sprinkler, when run in reverse will not spin, but why? I’ve heard various explanations that are either confusing, misleading, or wrong, so I wanted to tackle it myself.
What’s the big problem anyway? Why is this so hard to wrap your head around? I think the core of the confusion is that we have a problem which appears to be symmetric, and in physics, we expect symmetric situations to behave symmetrically. But, in fact, the symmetry is an illusion. Why? We’ll get to that…
First, I’d like to begin the analysis with our trusty friend, the control volume. Again, we have to be careful; this analysis has given me considerable trouble due to silly assumptions that I’m used to making, but cannot be made here.
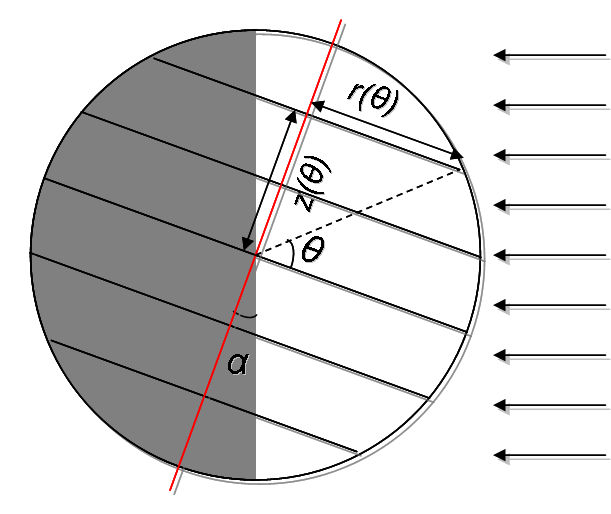
All right, first let’s start with the easier case: that of a sprinkler running in the “correct” direction underwater. To simplify the problem, we will assume the sprinkler is not moving or accelerating or anything. Speaking of symmetry, we’re going to use it here, and only examine half of our sprinkler:
Here’s a cross-section of the sprinkler; so let’s set up a control volume around the outside of the sprinkler pipe, across the entrance and exit. Here’s our scary-looking equation:
Okay, let’s start rocking the terms. Since we only care about the static state, we can drop the time-dependent term:
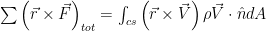
Because I’ve set up the problem so elegantly, everything happens at right angles and the cross products can simplify so that we are simply balancing torques perpendicular to the page:
The first term is equivalent to the total torque being applied to the control volume, while the second term comes from evaluating the integral for the flow out of the nozzle (top of the diagram). This is the only flow in our problem happening at any distance from the pivot point. The inflow is occurring at the axis of rotation and so it doesn’t contribute anything to the fluid’s angular momentum about that point.
Our job is now to equate the total torque with the torques on the control volume’s surface. Anything left over must be due to the external torque needed to keep the sprinkler still while water is flowing through it.
Generally, the torque is calculated by integrating 
over the control surface, where 
is determined by 
. It so happens for this type of finite control volume analysis, it works best to assume that the nominal fluid pressure is zero. This “gauge” pressure can be set arbitrarily without affecting our results, so for convenience (and to reduce the number of integrals we have to do), we will set it to zero, and fluid pressures will all be relative to this. That is, all of the surrounding, unmoving fluid in the problem will have a pressure of zero. Furthermore, in fluid mechanics, a “free jet” such as the one we have here, has a pressure equivalent to the surrounding fluid (that is, zero).
Soooo…. that means the pressure, and therefore the force all around the control volume is zero; which means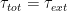 
and we have
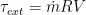
So the torque required to keep the nozzle in place is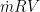 
(positive, out of the page). Another way to look at it is that this half of the nozzle apparatus (everything in the control volume) is exerting a torque of 
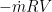on the hub, or whatever is holding it in place. Doing the same analysis on the other half would yield the same result, with the additive, total torque required to keep the sprinkler still equal to 
.
Have I lost you yet?
Okay, then; let’s keep going.
Here we have the case of the reverse (Feynman) sprinkler. It seems like a straight-forward process to redo the calculations, but with opposite flow conditions, but unfortunately some of our more essential assumptions break down. I think this is what creates confusion — a lack of symmetry in the flow.
A low-hanging fruit is that the pressure of the inflow is not equivalent to ambient in the reverse case. This can be worked out using the Bernoulli equation to determine pressure as a function of velocity, where along a streamline, (specific) energy is conserved:
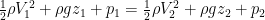
Since the fluid is being accelerated from the quiescent surroundings (which are at zero pressure), and change in elevation is negligible, the equation becomes:
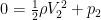
All right, I haven’t been entirely upfront with you. This is not a great application of the Bernoulli equation.
Where did we/I go wrong?
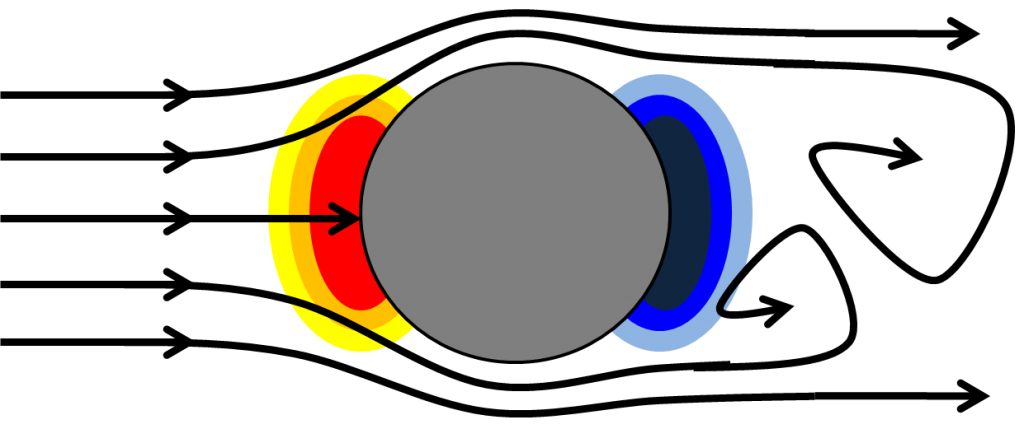
My cartoons have not been doing the flow field justice. The velocities at the exit probably look closer to this (regular sprinkler on the left, reverse sprinkler on the right):
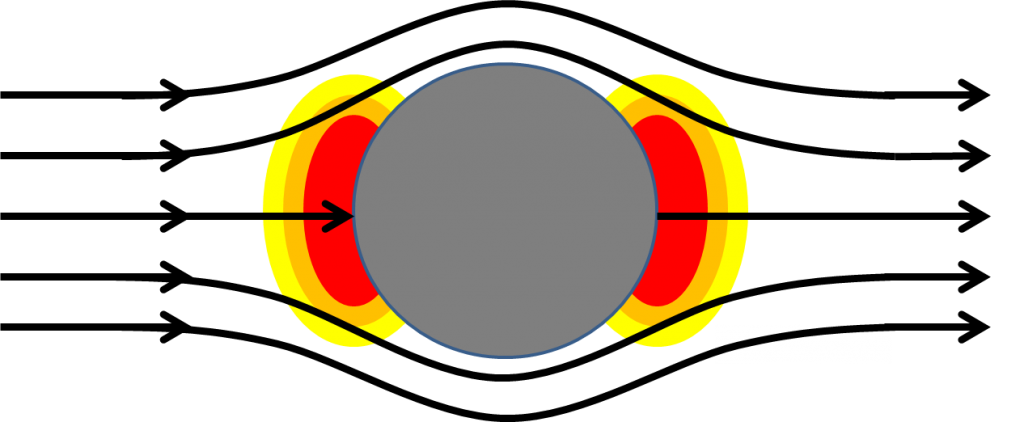
Another illustration of the non-intuitive asymmetry of the problem
The outflow velocities can more or less be considered to be parallel, and have an either laminar or turbulent profile, resulting in our expression for torque being mostly unchanged. However, I don’t have any good analytic expression for the velocity profile coming in, making our control volume analysis exceedingly difficult (I know there’s a vena contracta and separated flow as the fluid enters the nozzle). Since we’re assuming the mass flow rates are the same, though, I’ll take a leap of faith and say that right hand side of the control volume equation is the same in both cases (the velocity is the opposite direction, but the sign stays the same because it is squared).
But let’s use our new information to do a better job with the Bernoulli equation. When streamlines are bent so severely, some of the Bernoulli assumptions about conserved energy (inviscid-ness) are violated. This energy loss can be accounted for by introducing a head loss term:
where
What of this 
? It is a loss coefficient that is a function of the geometry of the loss feature; in our case the nozzle entrance. Similar “re-entrant” pipes tend to have very high coefficients, approaching the maximum of unity. Supposing it is unity, let’s recalculate the pressure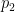 
:
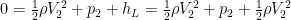
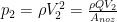
I’m sick of caveats, but here’s another one. The pressure is not uniform across the entrance, nor do the losses happen at the entrance. The pressure drop actually occurs due to viscous effects in the separated flow along the entrance of the pipe; but since we’re assuming inviscid flow, this is the correction we need to apply to the upstream pressure (at the entrance) to overcome these viscous losses.
We can then determine the torque from surface forces:
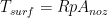
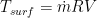
And now to work it in to our full control volume equation:
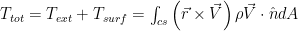
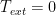
So that means there are no outside torques needed to keep the nozzle in place; in other words, the nozzle is not going to spin even if we don’t hold it.
Do I have you convinced?!
Although Feynman never revealed “the answer” or what happened when he tested it out in the lab, the general consensus is that there is no torque on the reverse sprinkler. However, knowing the answer definitely helped me get here, and I’m not sure that I can be totally confident in my assumptions. That being said, the flow profile, and therefore the analytical solution, is pretty messy in the reverse case, and requires some bold assumptions to make the problem tractable. Even if this explanation is not a concrete proof, I hope it helps align the math of the problem with experimental results. It certainly helped me rationalize the phenomenon.
, and linear density, 
, the length of a wire is inversely proportional to its frequency. That rings a bell; now if we (incorrectly) assume all of wires have the same tension and linear density, we can reconstruct the trend of the wire lengths as a function of piano keys, once we know the 
) are used to predict the drag force experienced by an object with frontal area at a particular fluid density and speed:
per 
for 
:
. At the equinoxes, 
. Daylight also depends on your latitude, 
, so I’ve included that, as well as dependent values 
and 
.
will be the difference in degrees of Earth exposed to daylight from our baseline 
. It can be determined as
is the radius of the Earth. Finally, we just need a last diagram to indicate the revolution of Earth around the sun.
marks the Earth’s position as it revolves around the sun, with the northern hemisphere experiencing summer solstice at 
, then we can say 
. Substituting into our equation for 
, we find![\beta=sin^{-1}\left[tan\,\theta\:tan\left(\zeta\:cos\,\phi\right)\right]](http://s0.wp.com/latex.php?latex=%5Cbeta%3Dsin%5E%7B-1%7D%5Cleft%5Btan%5C%2C%5Ctheta%5C%3Atan%5Cleft%28%5Czeta%5C%3Acos%5C%2C%5Cphi%5Cright%29%5Cright%5D&bg=ffffff&fg=000000&s=0 "\beta=sin^{-1}\left[tan\,\theta\:tan\left(\zeta\:cos\,\phi\right)\right]")
(we’re switching to radians!) is the angle spanned by sunlight, that means the daylight hours number:
and time of year ![12\;hrs \:\left(1+\frac{2}{\pi}\:sin^{-1}\left[tan\,\theta\:tan\left(\zeta\:cos\,\phi\right)\right]\right)](http://s0.wp.com/latex.php?latex=12%5C%3Bhrs+%5C%3A%5Cleft%281%2B%5Cfrac%7B2%7D%7B%5Cpi%7D%5C%3Asin%5E%7B-1%7D%5Cleft%5Btan%5C%2C%5Ctheta%5C%3Atan%5Cleft%28%5Czeta%5C%3Acos%5C%2C%5Cphi%5Cright%29%5Cright%5D%5Cright%29&bg=ffffff&fg=000000&s=0 "12\;hrs \:\left(1+\frac{2}{\pi}\:sin^{-1}\left[tan\,\theta\:tan\left(\zeta\:cos\,\phi\right)\right]\right)")
latitude is north of the arctic circle, resulting in continuous daylight and nightfall for parts of the year. By inspection, most of the curves (the U.S. spans approximately from 
to 
north) have their maximum rate of change at the equinoxes, which kind of makes sense; that is the midway point between the two solstices. The 
