More surface area, but it’s smoother.
Jamie Hyneman
Ba-ZOO-ka.
It’s fun to say!
Last week (with the walking in a straight line) was great, but there wasn’t a lot for me to break down, science-style. So I went back to the archives and dug up this beauty which aired recently while I was out of town. I’d like to concentrate on the bike part of the myth for now. Although, perhaps, they don’t have the technical background or terminology to exactly describe it, Adam and Jamie have a good feel with the major source of drag with an upright bicyclists.
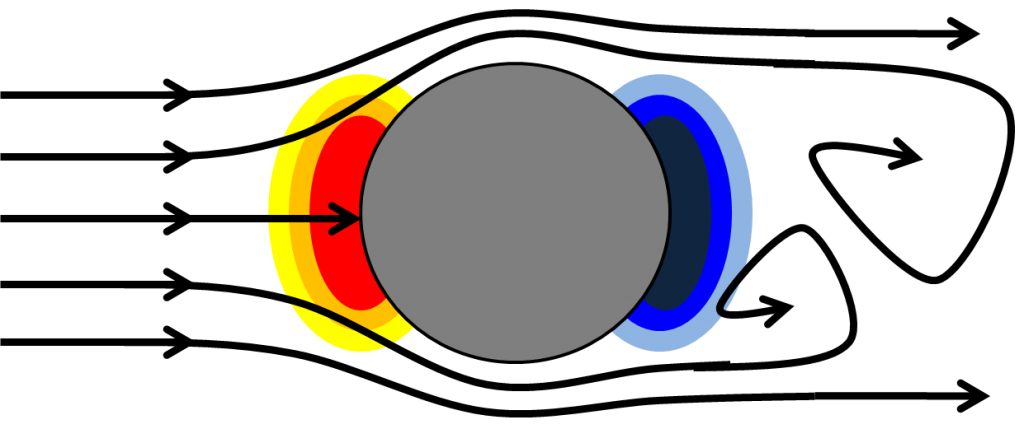
In general, there are two types of aerodynamic drag. One, called pressure drag is probably the intuitive kind that you’d typically think of when considering aerodynamic drag. You can think of it as happening when an object is moving so quick through a fluid (gas or liquid), that the fluid doesn’t have the ability to fill in behind the object as it passed by. Thus, a high pressure builds up on the front of the object and a low pressure on the backside. This pressure differential integrates across the surface of the body to produce a net force resisting the object’s movement (to the right in the image below).
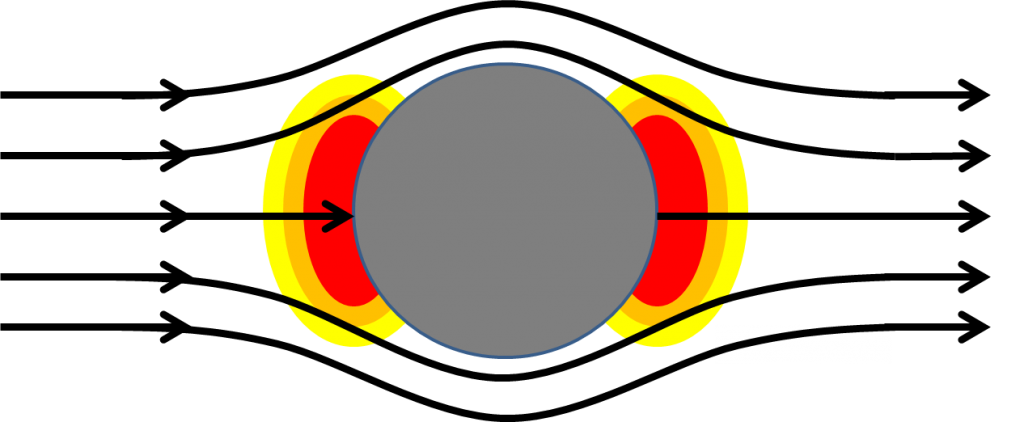
However, sometimes an object travels relatively slowly through a fluid, such that the fluid can recover and flow smoothly around the object’s backside (fluid dynamicists quantify this relative velocity with the Reynolds number). When this is the case (that is, the object is “streamlined” for the relevant Reynolds number), pressure drag can actually contribute very little to the drag force. Friction drag will become the dominant drag force, which is a function of the velocity of the object through the fluid, the viscosity of the fluid, and the surface area of the object.
I bold for emphasis, because in the case of the bike, Adam and Jamie keep the first two quantities constant and tweak the last one; that is, the motorcycle travels the same speed, through air, but now the geometry has mostly eliminated pressure drag, but greatly increased friction drag by increasing the surface area of the object.
from Wikipedia
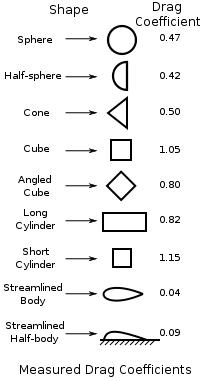
Engineers account for the two types of drag when calculating/measuring an object’s drag coefficient. While it may be intuitive to shape a body aerodynamically, making it “streamlined”, there is quite a bit of information about how easily basic shapes travel through the air. Sure enough, Adam and Jamie’s teardrop shape ranks quite low on this list of drag coefficients from Wikipedia.
These drag coefficients (
Of course, nothing can be so simple as that, and as it turns out,
I know that was kind of a lot to digest, so please feel free to continue the discussion in the comments!
Think about a rowers oar. as it quickly moves through the water a static head pressure is formed on the paddle face. The result is that instead of “catching” water the rower’s oar slips through the water because the static head creates a virtual streamline body on the face of the paddle! Now consider a modification to the oar’s paddle face. Add a few holes of a calculated size in the center of the paddle face, just big enough to disturb the formation of static head at that critical time when leg power is at the maximum. The result is no slipping and increased resistance for which the rower can apply the full power of their legs more effectively. You can prove this with a straight line arrange of spheres in a constant velocity flow and then vary the distance between the spheres from zero (I.E., touching) to infinity.
This is actually a fantastic point (if I understand you correctly). It reminds me of my swim team days. Learning technique for our pulls, we were taught to slightly space our fingers — just enough to increase the effective frontal area of the hand, but not so much that resistance drops as water passes freely between the fingers.
Here’s an article I found quickly that talks about it:
http://www.beginnertriathlete.com/cms/article-detail.asp?articleid=2510