There’s nothing remarkable about it. All one has to do is hit the right keys at the right time and the instrument plays itself
Johann Sebastian Bach
I found myself recently staring down into a baby grand piano recently, and for the first time I considered the motivation for its exterior curves. Noting the varying lengths of the piano wires for the different notes, I naturally assumed that their arrangement dictated the piano’s shape. A little physics, as well as piano history set me straight.
First off, I used Wikipedia to refresh my memory on how to calculate the fundamental harmonics of strings, which after a little rearranging, allows me to calculate a piano string/wire’s length:
So, for a given tension, 
Note that since the values I used for tension and linear density are arbitrary, the units of length are unimportant, just their relative magnitudes.
Now compare to the inside of a piano:
Not bad, right? Of course, there are some important differences that should be noted. First, the piano strings are in fact not of constant linear density or tension. Apparently, the linear density changes throughout the piano; I read somewhere that approximately every sixth string the wire gauge changes. The tension is obviously varied in order to get precise tuning. And the lower notes on the left hand side are rearranged completely differently, significantly changing the shape of that end of the piano. According to this article on piano history:
Overstringing was invented by Jean Henri Pap during the 1820’s and was first patented for use in grand pianos in the United States by Henry Steinway, Jr. in 1859. When overstringing a piano, the strings are placed in a vertically overlapping slanted arrangement, with two heights of bridges on the soundboard instead of just one. This allowed for larger strings to fit within the piano case.
So to avoid the long tapering spike at the lowest notes, it appears that as a matter of convenience, they are angled to help improve the overall footprint of the piano. I imagine their linear density is also significantly larger than the higher notes in order to reduce their length.
While I was dubious about it to begin with, it appears that in fact, there’s no justification for the inflection point that a typical piano has in it’s exterior. It’s simply an artifact of the arrangement of the lower notes, and probably aesthetics.
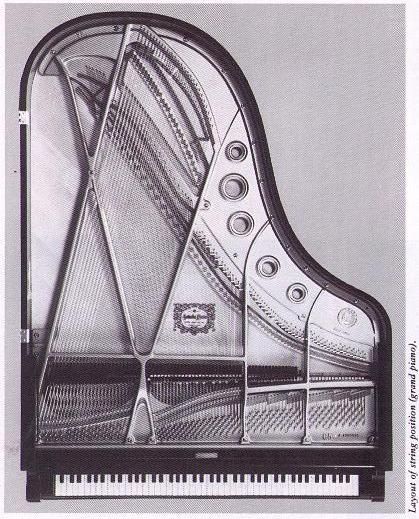
Piano design is full of compromises – and the smaller the piano the greater they are. String length is a major compromise. If the lower strings were their ideal theoretical length then the piano would be around 25′ long. This is obviously not practical – so the bass strings are overwound with copper to increase their linear density and foreshortened. The penalty for this is that the string becomes stiffer which results in the harmonics being not quite binary multiples of the fundamental – they are slightly sharp – which means that the tuning of the piano has to be “stretched” slightly so that these harmonics better coincide with the upper notes. Overstringing allows for both a longer bass string length for a given case size, and also puts the acoustic termination of the string nearer the (more sensitive) center of the soundboard for better tone….which brings us to the other dictator of piano shape – the soundboard design. Apart from the obvious string length influence on the piano shape the other influence is the desire to have the soundboard more or less symmetrical about the bridges – the long bridge in particular – and if you look at your photo you will see that this is more or less achieved. What isn’t apparent is that typically there is a bass cutoff bar (length of wood) underneath the piano attached to the soundboard that runs at about a 45 deg angle located, in your photo, at the bottom left. This effectively provides an acoustic termination of the soundboard essentially parallel to the long bridge- and at about the same distance from it as the rest of the piano rim. Reason for all this is that if the soundboard were allowed to get too big then it starts to become less efficient, and mechanically harder to control without collapsing!