The energy from the bullet’s impact has to overcome the merry-go-round’s inertia
Grant Imahara

The Mythbusters are back and so am I!  Even if I am 6 days late… but still before the next episode!  And it appears they have not hired a science consultant yet; so if they’re busting Hollywood for playing fast and loose with physics (experimentally), then I’m going to set them straight on theory.

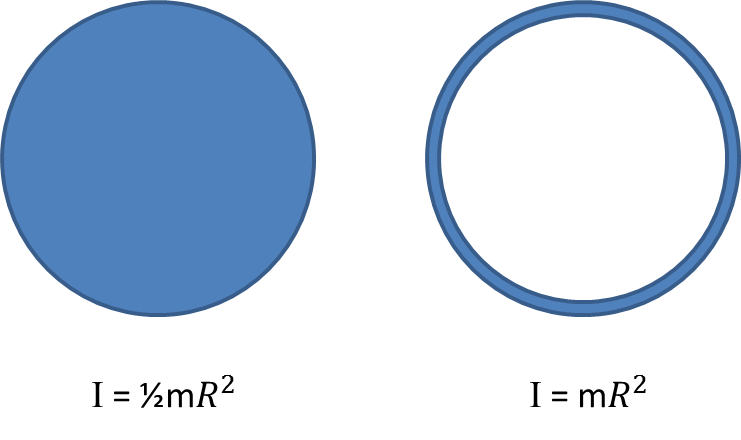
Grant (and the narrator) assume it is the merry-go-round’s inertia (which is related to its mass) that resists being spun by the bullet’s impact.  Rhett Allain actually did a pretty good demonstration of this (actually, his daughters are the ones who did the demonstration).  The mass/weight of the merry-go-round is nearly irrelevant.  Since it is rotating instead of translating, it’s the moment of inertia that is important.  For a given mass, depending on how it’s distributed throughout the merry-go-round, the moment of inertia will vary.

For instance, compare the moment of inertia for a merry-go-round with evenly distributed mass versus all the mass on the outer circumference.  A factor of 2 difference!

So according to the Mythbusters, these two merry-go-rounds have the same inertia, since they have the same mass and will respond the same to a bullet.  I beg to differ.  Depending on how that 500 lbs is distributed it will be easy (if the mass is near the center) or hard (if the mass is near the circumference) to spin.

How will they behave?  We can go about figuring this out in a number of ways.  One simplifying assumption would be to say the bullet gets lodged in the merry-go-round so that we know its behavior before and after impact.

If we knew how long the impact lasted, we could back out the force maybe, and then use the rotational version of to determine the angular acceleration (and subsequently, the angular velocity) as it relates to torque, :

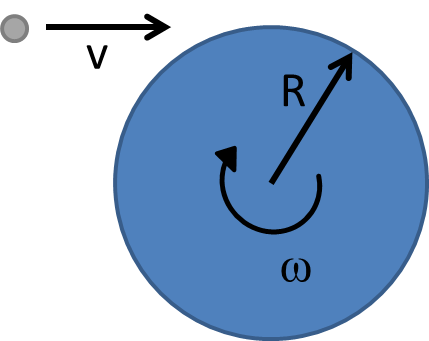
That’s too messy; we only care about the beginning and end states; conservation laws are great analysis tools for that.  I always prefer to solve such things with conservation of momentum when possible.  I’m not sure why; it just seems tidier to me.  Let’s say we conveniently measure the angular momentum around the center of the merry-go-round.  Before impact, the only contribution will be the bullet, which, solving for angular momentum, equals:

where is the radius of the merry-go-round, is the mass of the bullet, is the velocity (1300 ft/sec) and the direction is perpendicular to the plane of the merry-go-round (down towards the ground).  The merry go round will have the same angular momentum after being hit (before friction slows it down).  It’s angular momentum, will be the same as the angular momentum before the impact, so

See?  Very clean!  C’mon Mythbusters.  You can DO this!

Finally, as an aside, I’ll bet if Jaime and Adam were more committed, and they shaved off their facial hair, those masks would have fit a lot better…