Happy belated -day!
A friend of mine recently posted a question online about how a ping pong ball might be affected by altitude. Of course, once I got thinking about it, I decided the physics involved deserved its own post.
Of course, the drag, being a linear function of air density, is going to be affected by altitude. Using the barometric formula, we can calculate density as a function of altitude (I’m going to ignore the lapse rate, because I don’t need that sort of complexity in my life):
where is altitude; I’ll assume normal atmosphere, with
and
.
All right, drag is the low-hanging fruit, simply affecting how quickly the ping pong ball will slow down. At higher altitudes, a ping pong ball should travel further than it would at sea level, all else being equal. This is nothing new, right? When the Rockies first showed up in Denver, it was running joke for years how “easy” it is to hit home runs in Denver because of the “thin” air. At 5,000 feet, the air is about 83% as dense, so the balls should fly almost 20% further! Certainly nothing to sneeze at!
But ping pong is a game of spin, no? The really interesting forces to consider are the aerodynamics forces as a result of spin. Of course, there are not limited to ping pong — pitchers in baseball rely on spin to affect ball movement; tennis players, like ping pong players, use spin to make sure a well-struck ball lands in-bounds; some of us slice golf balls into the woods; “Bend it like Beckham”, anyone?
Okay, so spin is obviously an important factor in influencing the trajectory of a ball in flight. But how? Why?
Enter Herr Heinrich Magnus.
His work researching the deflections of projectiles earned him the privilege of having his name attached to the effect on a circular body rotating as it moves through a fluid. As I snooped around trying to find the best way to explain this force, I was struck that its misunderstood in a way not unlike how airfoils are sometimes mis-described.
Many people make assumptions about the speeds at which air travels around airfoils, and use Bernoulli to explain lift and drag; the simpler, and more accurate answer to the question of lift of airfoils or rotating cylinders often lies with momentum conservation. Airfoils deflect air downwards, therefore they must be pushed upwards; rotating bodies will feel a force opposite the direction in which the push the air moving past them.
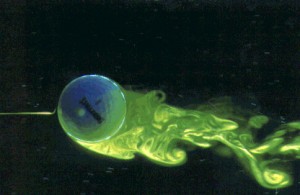
A good way to think about how the momentum is changed is boundary layer separation. Notice in the image, that once the boundary layer separates from the front, top side of the airfoil (made visible with streaklines), it continues more or less straight back, and the flow coming off the bottom of the underside of the airfoil actually tends upward once it leaves. In normal operation (not stall, like this airfoil appears to be experiencing), that flow would stay attached to the top part of the wing and travel backwards and downwards. The downward momentum imparted causes lift in the airfoil. Once detached, the airfoil cannot impart any momentum nor receive any lift.
All right, we’re to the home stretch of the nitty-gritty stuff. There are 4 ways this can go down depending on the speeds, fluids, etc. involved.
- No separation
- Laminar-laminar separation
- Turbulent-turbulent separation
- Turbulent-laminar separation
If everybody plays nice, and the ball moves very slowly through the air, the boundary layer can stay attached for the whole ride to the back of the ball. This actually lends itself well to potential flow analysis, using a doublet and vortex, but without opening that can of worms, suffice it to say that the air will have an upward velocity component as it moves away from the ball, and the ball will experience a downward force.
If the ball is moving through the air at a slightly brisker pace, the flow will separate on both sides. but because the relative motion of the ball and air is greater on the top, it will separate further upstream than on the bottom. The air on the bottom will be more strongly redirected upwards than the flow on top will be deflected downwards, resulting in an overall downward force applied to the ball.
If the ball is moving at a brisk pace through the air (or has a rough surface), turbulent boundary layers will develop on both sides of the ball. These will stay attached longer than their laminar counterparts, all else being equal (remember why golf balls have dimples?), but ultimately, they will succumb to the same fate, with the upper layer detaching first, resulting in a downward force. This is what happens to most sports balls, as they have seams or fuzz or whatever to cause turbulence (and therefore less overall drag).
BUT, if all the elements conspire: a smooth ball with just the right rotation moving through the air at just the right speed, what can happen is that the faster relative motion of the top of the ball causes the top boundary layer to become turbulent, while the bottom layer stays laminar. The upper boundary layer then has a chance to stay attached longer than the bottom since it’s turbulent, giving it more downward momentum, and causing lift! This is opposite what is traditionally thought of as the direction of the Magnus force, but does happen; just maybe not in ping pong (I’ve never observed topspin causing lift during a game…).
Oh yeah, ping pong. I guess I got myself a little side-tracked there. Via Wikipedia, there is a tidy little formula for estimating the effect of the Magnus force:
This indicates not only that the force is perpendicular to both angular velocity of the ball and the velocity of the free stream air, but also that it is not dependent on air density. Well, I’ll bet that factor is not unlike the coefficient
used to calculate drag, which is dependent on the Reynolds number which is itself dependent on the density.
So I hope you enjoyed that wild ride of a detour about the Magnus effect. Since I don’t know much about my coefficient , I’m afraid I can’t say much about the effect altitude will have on the Magnus effect, but I’ve got to believe that it will play a non-negligible role, considering the density differences.
If you want to get in touch with your academic side, I consulted these two papers for additional insights:



hello, very nice work.
Question:
if the ball IS NOT SPINNING and say tethered with a very light string for example, and a 10-20 MPH Wind is blown straight at the ball ,( i tried to lower the variations for you) would the ball rise or stay the same. NO SPIN..
Thanks, i am working is a area that balls, domes, and lift bodies.
alex kattas hope to get the answer because, i still only see
” When the ball is spinning as it dos when plying Ping Pong.