We never believe the math on Mythbusters.
Adam Savage
Well, Adam, that’s what we’re here for. After just a little explanation, the most difficult thing about buoyancy is spelling it correctly. The Mythbusters gave a couple great examples in a single episode (Ping Pong Rescue; November 3rd, 2004) with ping pong balls and helium-filled balloons. The show was, as usual a little short on explanation; we’ll try to remedy that here and now.
Buoyancy Review
If you’re going to take away one thing from this post, it should be that it’s really quite straightforward to think about floating vs. sinking. Just visualize the object in question. Then imagine the amount of water it is going to displace (generally equal to the object’s volume). If the object weights less than an equivalent volume of water, then the object will float; if it is heavier, it will sink. This also applies to objects in air, it’s just that
Then imagine the amount of water it is going to displace (generally equal to the object’s volume). If the object weights less than an equivalent volume of water, then the object will float; if it is heavier, it will sink. This also applies to objects in air, it’s just that
- there aren’t a whole lot of objects that are “lighter than air” and
- the “weight” of something becomes a little hazier in that regime (negative weights are sort of counter-intuitive)
Hence, both the ping pong and balloon myths are both myths about buoyancy!
For an object that sinks, its effective underwater weight (if you were to put it on a scale while submerged) would be its above water weight minus the weight of displaced water. This is why the guys ended up buying too many ping pong balls. Not that it was a bad way to cover their butts, because by buying enough ping pong balls to lift the “dry” weight of the boat, they were addressing the upper bound of their ping pong needs. If the boat had been crushed to an very small volume, you would have needed a lot more ping pong balls. Because it displaced quite a bit of water, it had a relatively low “wet” weight which the ping pong balls needed to offset.
Not to spend to much time on this point, but how about a quick example? For instance, if you pulled an iceberg out of the ocean and weighed it, with Adam’s method you would estimate that you’d need a gaggle of ping pong balls to float it. Of course, it will float without a single ping pong ball, which hopefully stresses that buoyancy should be taken into account for any such calculation. In fact, to determine if any assemblage of objects will float or sink, simply add the volumes and weights of the objects and see if that is heavier than the total equivalent volume of water.
To the math!
Ping Pong Balls
Suppose a ping pong ball has a mass of 2.7 grams (0.006 lbs) and a diameter of 40 mm (1.6 in). Then an equivalent volume of water would weigh  , for a net buoyancy of 0.071 – 0.006 = 0.065 lbs. Just as Adam said, it would take
, for a net buoyancy of 0.071 – 0.006 = 0.065 lbs. Just as Adam said, it would take  to buoy the 1 pound of shot. The difference is, I trust the math.
to buoy the 1 pound of shot. The difference is, I trust the math.
For their 3,500 lb boat, Mythtanic II, let’s take a stab at how much water it displaced. Since it took 26,000 ping pong balls:
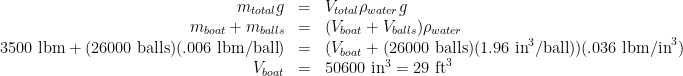
So, the boat displaces about 29 cubic feet of water (whether floating or sinking). Any boaters out there who can tell me if that number seems reasonable?
Packing Spheres
Adam spends a little bit of time talking about how efficiency ping pong balls pack together. Of course, he doesn’t ask how efficiency can ping pong balls pack together, but let’s answer that question, anyway. Unfortunately, while they show him measuring up the aquarium and punching into his calculator, they don’t actually shed any light onto the numbers he got, except to say that he got a 51% packing efficiency.
A great number of people have looked at this problem before us, and when it comes to packing spheres, there are a couple of methods of arranging them that will net 74% packing efficiency (see Wikipedia: Close-packing of spheres). Of course, one has to be careful, and consistent on how the spheres are packed, and surely, when the boat is floated, we cannot count on any sort of optimal packing efficiency. So in that sense, Adam’s more empirical method probably gives a better sense of what the actual packing efficiency will end up being (and we’ve already checked its reasonableness by comparing it to the maximum possible packing efficiency).
Balloons
While the crew takes a reasonable approach to trying to figure out how many balloons they’ll need, they are at a disadvantage to Adam and Jaime inasmuch as the volume (and therefore buoyancy) of a ping pong ball is very consistent and predictable, a balloons buoyancy will vary quite a bit depending on how well its inflated. That is, as the volume of each balloon varies (depending on how “full” its filled), its buoyancy will vary. So it is no surprise that they do not have a lot of success predicting how many balloons they would end up needing. Furthermore, the harness and rope needed to connect the balloons together and to the child are sure to increase the final balloon count. Judging that ultimately, they had the balloons and time needed, they were aware that their estimate may have undershot the eventual requirements.
Flowing Ping Pong Balls Down
This could be interested to look at, but I’m running out of steam for this one show. Anyone interested in examining the physics of moving the balls down to the boat just needs to estimate the velocity of water needed to provide a force that will cancel (or exceed) the force of buoyancy (hint: both of these forces are essentially independent of depth).
Even More Science
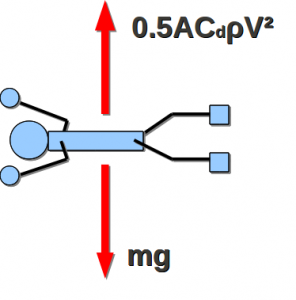
Objects experience buoyancy when they are immersed in a fluid subject to hydrostatic pressure. That means, as you move down in the fluid, the pressure increases, due to the extra weight of all the fluid above it. Water is a really straightforward example of this, because it’s essentially incompressible, so it’s easy to calculate pressure as a function of depth; it increases linearly as depth increases:  . The atmosphere, being compressible, can be a little more complicated, especially since we start at the “bottom”, so we’ll concentrate on buoyancy in water.
. The atmosphere, being compressible, can be a little more complicated, especially since we start at the “bottom”, so we’ll concentrate on buoyancy in water.
Of course, when Adam and Jaimie imploded the ping pong balls in their pressure chamber, the balls didn’t start floating (because ping pong balls don’t float in “regular” air). So it’s not just increasing the static pressure that makes objects float. It’s the incremental increase of pressure with depth that exerts an upward force. Basically the surface on the bottom of the object is experiencing higher pressure than the surface on the top, leading to a net upward force.
 Look at the simple example of a submerged cylinder. The top surface of the cylinder is experiencing a pressure of
Look at the simple example of a submerged cylinder. The top surface of the cylinder is experiencing a pressure of  , while the bottom surface is experiencing a pressure of
, while the bottom surface is experiencing a pressure of  (the sides of the cylinder are irrelevant, as the pressure on them acts perpendicular to gravity and ultimately cancel each other out). Or, doing a force balance in the z-direction, the net force on the cylinder is
(the sides of the cylinder are irrelevant, as the pressure on them acts perpendicular to gravity and ultimately cancel each other out). Or, doing a force balance in the z-direction, the net force on the cylinder is

A-ha! We have a net force that depends on the weight of the cylinder, the weight of an equivalent volume of water, and it is independent of the depth!
If you care to imagine it, this can be generalized to an arbitrarily shaped object simply by building the object out of a very large number of very small diameter cylinders (better yet, square prisms so there are no gaps in between!) that extend from the top of the object to the bottom. The sum of the forces will come out the same (assuming you use skinny enough cylinders).
– length of the car
– velocity of the car
– density of water (or whatever liquid we’re trying to skip)
– mass of the car (assume for simplicity, it’s distributed consistently throughout the car)
(square of the Froude number) and
(sort of a specific gravity). We want them to be the same in both the large and small scale tests. There are a couple things we’re stuck with. Since the car is scaled 1:12, it is, let’s say 1 ft (0.3 m) long instead of 12 ft long. And gravity isn’t going anywhere, so we’re stuck with
. Maybe we could use a different liquid, but we’ll stick with water for now, so
. So that only leaves our new speed and new mass (note, 50 mph = 22 m/s and 2600 lbm = 1200 kg):
=
=
and
. What do you know? That was the velocity and mass they used! That means they used science! And since they had no explanation of why they did what they did, they left me something to talk about. FTW!


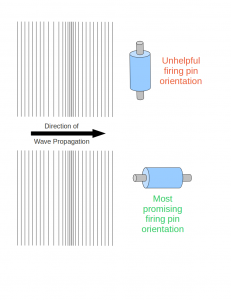 The other problem with their experiments is that they often aligned their guns perpendicular to the sound waves that were hitting them. Acoustic waves are longitudinal waves, which means they transmit energy in the same direction in which they move. In order to “accidentally” fire a gun, the pin needs to line up with the wave propagation direction. Oftentimes (most egregiously, in the sound chamber they used), the gun in question is lined perpendicular to the acoustic wave propagation, meaning there is no impetus for the pin to move along its axis. Think about getting a
The other problem with their experiments is that they often aligned their guns perpendicular to the sound waves that were hitting them. Acoustic waves are longitudinal waves, which means they transmit energy in the same direction in which they move. In order to “accidentally” fire a gun, the pin needs to line up with the wave propagation direction. Oftentimes (most egregiously, in the sound chamber they used), the gun in question is lined perpendicular to the acoustic wave propagation, meaning there is no impetus for the pin to move along its axis. Think about getting a