Satisfying ding isn’t it?
Adam Savage
It is, it is. But not as satisfying as them crashing cars to debunk Jamie’s reckless statements about car smashing from a few (episodes? years?) back. Ok, it wasn’t that bad. However, I think it doesn’t take much reflection to realize that the collision of two cars going 50 mph in opposite directions is the same as one car crashing into a stationary car at 100 mph, or one car crashing into a rigid wall at 50 mph. As much as I liked the follow-up, I got kind of tired of Adam expressing his amazement and confusion of this fact.
Although they didn’t wade too deep into the math, I was also impressed that they noted that when a car doubles its speed, it quadruples its kinetic energy, thanks to ). I also wish they dipped into the math a little more when they did their very clever small scale test with pendulums of clay sandwiches. Then again, if they did, I’d have nothing left to do…
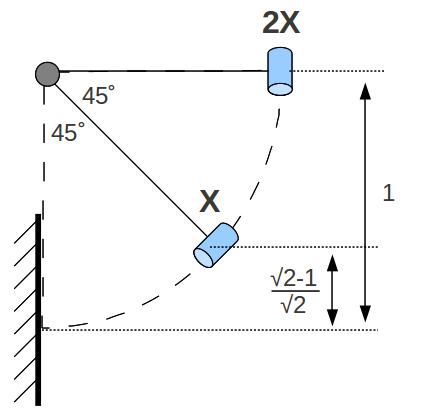
So since they are released from a height with zero velocity and swing down to the zero height from which we are calculating potential energy, it is safe to say that the pendulum cars are converting all of their potential energy into kinetic energy:
When doing these sorts of calculations, especially when comparing relative magnitudes with no need for precise quantification of the actual velocity, it’s useful to use unity as a value for unknowns that both objects have in common. For instance, I’ve gone ahead and deemed the height of the 2X velocity car is unity (making the height of the speed X car ). Once we cancel out the masses, we have for speed X:
and speed 2X:
So the resulting 2X is in fact:
Not quite twice as fast as the lower pendulum, but we’ll let them slide.
Knocking Socks
Again, I have to commend the team for tackling an old issue and its associated lingering questions. However, while they were thorough in many respects, I don’t think they were thorough in one of the more critical respects. The force of removal tests on Tori, for instance, were really neat. They appeared well-conceived and executed. And I have to admit, I think they’re right about knocking the socks off someone just wearing socks. However, in my experience, most boxers do not just wear socks. They also wear a little something I’ll call “shoes”.
The problem is that the team did not think hard enough about the mechanism by which socks are removed. To the extent I can put it in plain English: The removal of socks hinges on the inability of the accelerating foot to apply sufficient force to the socks to accelerate them at the same rate.
Imagine a worst-case scenario world, where while we’ve minimized friction force between the foot and sock (maybe some sweat would help in this respect), the friction between the sock and shoe is infinite. So in order for the shoe (and sock) to stay on the accelerating foot, the mass of the sock and the shoe must be accelerated at a comparable pace. This would take much more force (seeing as shoes weigh much more than socks, and all). So, perhaps a bit counter-intuitively, as long as the shoes weren’t tied on overly tight, and there was considerable friction between the socks and shoes, they would have had a much easier time knocking Buster’s socks off if they had just given him some appropriate footwear.