Dr. Allain wrote up a great post on this subject, so I’ll reduce the scope of what I was going to say, and let you read his analysis for the rest of the story. He used dot products for a much more elegant analysis than my trig-based approach.
I’ll focus on a more specific question pertaining to college football. With the has marks so much wider than the actual field goal posts, the angle that the kicker must aim for can be quite severe, especially close to the posts. My question is, is there a distance where it would behoove the kicker to kick from farther away (I don’t mean in order to move it more to the center of the field, I mean straight back)? Instead of snapping the ball 7 yards back from the line of scrimmage, maybe snap it back 10 or 12 yards. At the extreme hash, what is the optimum distance from which to kick to give yourself the best opportunity to make the field goal?
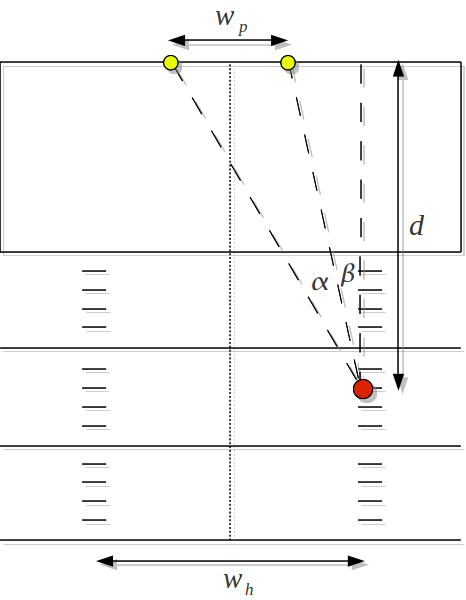
For our purposes, we will consider this a 2-D problem, where the height of the goal posts don’t matter. The kicker’s ability to make a field goal only depends on his aim. The wider the acceptable angle envelope (), the better the chances of making the kick.
In our diagram, let’s define . It is easiest to calculate
as
since
and
are easy to calculate as arctan’s:
To calculate the maximum value of alpha, we just take the derivative with respect to the field goal distance, . It’s a little hairy; I had to look up the derivative of arctan, do some variable substituting, but it beats integration. I ended up with,
which can be solved for after setting
to zero:
So the angle is maximized at
. Good, but unexciting result. That It means that it only makes sense to move straight back when kicking inside of 18.9 ft (~6.3 yards). That’s inside the end-zone. So forget I said anything… At least I don’t have to wonder anymore.