Warning: Science Content

Magnus Force

March 16th, 2011 1 Comment

Happy belated $\pi$ -day!

A friend of mine recently posted a question online about how a ping pong ball might be affected by altitude. Of course, once I got thinking about it, I decided the physics involved deserved its own post.

Of course, the drag, being a linear function of air density, is going to be affected by altitude. Using the barometric formula, we can calculate density as a function of altitude (I’m going to ignore the lapse rate, because I don’t need that sort of complexity in my life):

$\rho = \rho_0 exp \left[ \frac{-g_0 M z}{R^* T_0}\right]$

where $z$ is altitude; I’ll assume normal atmosphere, with $\rho_0=1.225 \tfrac{kg}{m^3}$ and $T_0 = 288.15 K$ .

All right, drag is the low-hanging fruit, simply affecting how quickly the ping pong ball will slow down. At higher altitudes, a ping pong ball should travel further than it would at sea level, all else being equal. This is nothing new, right? When the Rockies first showed up in Denver, it was running joke for years how “easy” it is to hit home runs in Denver because of the “thin” air. At 5,000 feet, the air is about 83% as dense, so the balls should fly almost 20% further! Certainly nothing to sneeze at!

Reposted from http://www.ecs.syr.edu/centers/simfluid/red/golfballpics.html

But ping pong is a game of spin, no? The really interesting forces to consider are the aerodynamics forces as a result of spin. Of course, there are not limited to ping pong — pitchers in baseball rely on spin to affect ball movement; tennis players, like ping pong players, use spin to make sure a well-struck ball lands in-bounds; some of us slice golf balls into the woods; “Bend it like Beckham”, anyone?

Okay, so spin is obviously an important factor in influencing the trajectory of a ball in flight. But how? Why?

Enter Herr Heinrich Magnus.

His work researching the deflections of projectiles earned him the privilege of having his name attached to the effect on a circular body rotating as it moves through a fluid. As I snooped around trying to find the best way to explain this force, I was struck that its misunderstood in a way not unlike how airfoils are sometimes mis-described.

Many people make assumptions about the speeds at which air travels around airfoils, and use Bernoulli to explain lift and drag; the simpler, and more accurate answer to the question of lift of airfoils or rotating cylinders often lies with momentum conservation. Airfoils deflect air downwards, therefore they must be pushed upwards; rotating bodies will feel a force opposite the direction in which the push the air moving past them.

Flow separation due to high angle of attack

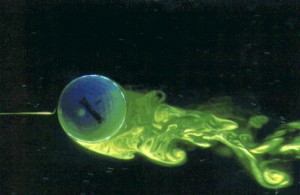
A good way to think about how the momentum is changed is boundary layer separation. Notice in the image, that once the boundary layer separates from the front, top side of the airfoil (made visible with streaklines), it continues more or less straight back, and the flow coming off the bottom of the underside of the airfoil actually tends upward once it leaves. In normal operation (not stall, like this airfoil appears to be experiencing), that flow would stay attached to the top part of the wing and travel backwards and downwards. The downward momentum imparted causes lift in the airfoil. Once detached, the airfoil cannot impart any momentum nor receive any lift.

All right, we’re to the home stretch of the nitty-gritty stuff. There are 4 ways this can go down depending on the speeds, fluids, etc. involved.

No separation
Laminar-laminar separation
Turbulent-turbulent separation
Turbulent-laminar separation

If everybody plays nice, and the ball moves very slowly through the air, the boundary layer can stay attached for the whole ride to the back of the ball. This actually lends itself well to potential flow analysis, using a doublet and vortex, but without opening that can of worms, suffice it to say that the air will have an upward velocity component as it moves away from the ball, and the ball will experience a downward force.

If the ball is moving through the air at a slightly brisker pace, the flow will separate on both sides. but because the relative motion of the ball and air is greater on the top, it will separate further upstream than on the bottom. The air on the bottom will be more strongly redirected upwards than the flow on top will be deflected downwards, resulting in an overall downward force applied to the ball.

If the ball is moving at a brisk pace through the air (or has a rough surface), turbulent boundary layers will develop on both sides of the ball. These will stay attached longer than their laminar counterparts, all else being equal (remember why golf balls have dimples?), but ultimately, they will succumb to the same fate, with the upper layer detaching first, resulting in a downward force. This is what happens to most sports balls, as they have seams or fuzz or whatever to cause turbulence (and therefore less overall drag).

BUT, if all the elements conspire: a smooth ball with just the right rotation moving through the air at just the right speed, what can happen is that the faster relative motion of the top of the ball causes the top boundary layer to become turbulent, while the bottom layer stays laminar. The upper boundary layer then has a chance to stay attached longer than the bottom since it’s turbulent, giving it more downward momentum, and causing lift! This is opposite what is traditionally thought of as the direction of the Magnus force, but does happen; just maybe not in ping pong (I’ve never observed topspin causing lift during a game…).

Oh yeah, ping pong. I guess I got myself a little side-tracked there. Via Wikipedia, there is a tidy little formula for estimating the effect of the Magnus force:

$\vec{F} = S\left(\vec{\omega}\times\vec{v}\right)$

This indicates not only that the force is perpendicular to both angular velocity of the ball and the velocity of the free stream air, but also that it is not dependent on air density. Well, I’ll bet that $S$ factor is not unlike the coefficient $C_d$ used to calculate drag, which is dependent on the Reynolds number which is itself dependent on the density.

So I hope you enjoyed that wild ride of a detour about the Magnus effect. Since I don’t know much about my coefficient $S$ , I’m afraid I can’t say much about the effect altitude will have on the Magnus effect, but I’ve got to believe that it will play a non-negligible role, considering the density differences.

If you want to get in touch with your academic side, I consulted these two papers for additional insights:

Flickering Flame

February 14th, 2011 1 Comment

This would be more appropriate as a Halloween post, and in fact, that’s what I intially intended, but I want to give you a head start; you need something to do now that Valentine’s Day is over!

I enjoy a jack-o-latern like anyone else; however, candles are consumable and potentially disastrous. I wanted a simple electronic alternative and wiring project. Random flickering is a hard thing to do. Especially without a microcontroller. I decided instead of dimming a light on and off, I’d have some background light, and the overall intensity would be modulated by turning on and off additional LEDs.

Unfortunately, I can’t find the forum that gave me the idea, but it’s as simple as setting up two 555 timers in astable mode and wiring an LED up in either direction as seen in the wiring diagram below. The diagram includes a modified version of the astable configuration I found in Make: Electronics. The extra diode allows for independent modification of the on and off time by changing $R_1$ and $R_2$ .

When both output pins (#3) are positive or negative, the LEDs will not light up, however when they are opposite, exactly one of the LEDs will light up (whichever diode is correctly polarized). You can experiment with the resistor and capacitor values to get different frequencies and on/off times. Here are the equations you’ll need; namely, frequency:

$f=\frac{1}{ln\mbox{ }2\mbox{ }(R_1+R_2)C_1}$

on-time:

$t_{on}=ln\mbox{ }2\mbox{ }R_1C_1$

and off-time:

$t_{off} =ln\mbox{ }2\mbox{ }R_2 C_1$

I hooked this up to +9 V with good results; I noticed that a different input voltage gave me a different response. I didn’t use any resistors in series with the LEDs because my 555 timers were current limited below the LED threshold. My $R_1$ resistors were $1.8 k\Omega$ each, and the $R_2$ ‘s were each $2.2 k\Omega .$ For capacitors, I had $C_1=47 \mu F$ and less importantly, I also had $C_2=47 \mu F$ . I used electrolytic capacitors because I had them lying around; of course, if you use ceramic capacitors, you need not worry about polarity.

There parameters gave me a frequency of a little less than 8 Hertz, and each was mostly split evenly between on and off (on slightly longer than off). Due to subtle differences in the resistors on each 555 timer (mine were only accurate to +/- 5%), the frequencies will be slightly out of phase. The asynchonous behavior yields a flickering that I found pleasant to the eye. I really haven’t played around with it that much, but it occurred to me that throwing in a photoresistor or something in parallel with one of the resistors could accentuate the randomness. You may also consider using a few potentiometers to make adjustments on the fly.

As I mentioned earlier, in addition to the two flashing LEDs, I had three additional on at all times. Because I didn’t have orange LEDs, I used four yellow LEDs and one red LED to get an orange, flame effect. I used a 9 volt battery to place it outside, inside a jack-o-lantern. For inside, I can place it into a “lantern” and hook it up to a 9 volt DC wall wart.

Forked

February 12th, 2011 No Comments

Wow. It’s kind of unsettling how quickly two weeks can pass in between posts. I don’t know how Dr. Allain finds the time to be so consistent posting to his blog.

One of the television programs that gets watched on in my house is Minute to Win It. You know, the 6 minute show they somehow stretch out to an hour with that annoying host with the terrible hair. Fortunately, DVR allows the show to be watched in under 10 minutes, as God intended.

Anyway, a lot of the contests they have challenge one’s skill, balance, concentration, etc. But when the stakes are high, the contestants are usually subjected to a game of luck. A recent case in point was a game called “Forked”. In this, the contestant is required to roll a quarter in between a fork tine from 16 feet away.

Now, this seemed kind of unfair, but I figured I’d calculate just how difficult it was.

First, we’ll see how hard it is just to hit anywhere on the fork. Then we’ll check out how precise one needs to be to lodge in a single tine. This analysis isn’t so different from the field-goal analysis from an earlier post. For our purposes, we’ll assume that once released, the quarter travels in a straight line.

According to the show, each tine is separated by $\tfrac{3}{16}''$ . I’ll assume that each of the tines is also $\tfrac{3}{16}''$ wide. The total span is therefore $\tfrac{12}{16}''+\tfrac{9}{16}''=\tfrac{21}{16}''$ .

What does $\tfrac{21}{16}''$ look like from 16 feet away? We’ll there are a couple of ways to do this, but I’ll rock a trigonometric approach, using the tangent operator to calculate the angular span of the fork from 16 feet.

$angle = 2 tan^{-1}\frac{21/32}{192} = 0.39^{\circ} = 24\mbox{ arcmin}$

Where the units mean 24 arc-minutes or 24/60th of a degree. I’m not sure what you make of this, but it seems small to me. Compare that to the span of the moon and the sun in the sky; they each span approximately 30 arc-minutes in the sky. So follow me here, but that means if we were to build a plank all the way to the moon/sun, it would be easier to roll a quarter to hit either of them (again, assume the quarter stays straight and can make it the whole way), than it is to hit the fork. Holy cow.

What about actually rolling it in between the space between two tines? Now, since the quarter has finite width (0.069″), the quarter actually only has $0.1875'' - 0.069'' = 0.1185''$ of play and still be entirely within each tine.

$angle = 2 tan^{-1}\left(\frac{0.1185/2}{192}\right)= 0.035^{\circ}=2\mbox{ arcmin}$

Ok, 10 times smaller! Granted, there are three such openings in which you can lodge the quarter, but you’d have to aim less carefully to roll a quarter between Jupiter and Europa!

(Algae) Population Growth

January 25th, 2011 No Comments

Boy, that escalated quickly… I mean, that really got out of hand fast.
Ron Burgandy

If you’ve ever kept an aquarium, you’ve probably worried about algae. If you’ve maintained a planted aquarium with powerful lighting, doubly so. The neat, sort of counter-intuitive thing, is that it is really quite possible to grow plants successfully under high-light conditions without running up against constant algae problems.

There are lots of ways to hash out algae control, and it’s debated all over the internet. I’ve read a lot about how plants may secrete some chemical to inhibit their growth; there are any number of anti-algae formulas you can buy to add to your tank; it’s said that the ratio or absence/presence of certain nutrients in the tank may favor algae growth (when it comes to phosphates, it seems the community has at different times phosphorous causes or inhibits growth). So it’s obviously confusing, and there is probably some truth in all of these claims.

For myself, I once tried to chase those solutions, but now I mostly concentrate on keeping my tank algae free by keeping my tank algae free.

That doesn’t make sense? Let me explain.

A very pregnant otocinclus

I needed some help with the details, but I remembered studying some population models and I’m always looking for an excuse to go all Runga-Kutta on a time-dependent ODE. Instead of using one of their standard models, I made one of my own! I wanted exponential growth, but instead of being bounded by resources, I wanted to account for the five otocincluses (otocincli?) in my tank. They’re known to be pretty good algae eaters; but their consumption should be relatively independent of the amount of algae in the tank; they’re small fish and can only eat so much!

Now, of course, there are a number of simplifications to my model, including that one. I’m going to lump all types of algae into a single category, and I’m going to modify my “devouring” constant, D, slightly, to make sure the fish aren’t eating more algae than exists in the tank…

$\frac{dN}{dt}=rN-D\left(1-e^{-kN}\right)$

where r is the rate of growth of the algae, and N is the population of the algae (say, number of colonies). Now, I’m going to use made-up numbers here (for instance, the time doesn’t have specific units), but they’re not important because I’m just trying to prove a point.

I used 4th order Runga-Kutta to solve this from t=0 to 1, using my favorite (free) Matlab emulator, Octave. For the sake of argument, I set r=1, D=1010, k=0.01, and I proceeded to examine different initial levels of algae. Hopefully the plot below helps clarify my earlier statement:

I hope it is clear that at the end of the time, the state of the algae population has a lot to do with its initial size. Assuming a more or less constant “devouring” rate, the algae population will flourish or die out depending on the size/number of established colonies. And that’s why keeping the tank clean is the best way to have a clean tank…

Reverse Engineering

January 18th, 2011 No Comments

…[O]ur barrier does not move so when our car carrying the surfboard hits it, it’ll come to a complete stop, and all that momentum from the car will be transferred to the surfboard.
Tori Bellacci

I want to give the Mythbusters some props for trying to introduce the concept of momentum; however I must instead scold them for completely bungling it. In the scenario they are testing, they want to see how lethal a surfboard is when flying from the roof of a car.

I’m not really sure what they think momentum is, but let me clarify. An object’s momentum, $\vec{p}$ is simply its mass times its velocity, $m\vec{v}$ . It is probably my favorite physics quantity because it is always conserved. That’s a very useful foundation for solving lots of problems. Anyway, does the car transfer any (or all) or its momentum to the surfboard?

Well, before it hits the barrier, the surfboard has x-momentum equal to its mass (let’s say 10 kg) and velocity (40 mph = 18 m/s):

$p_{1}=mv_{1}=(10 kg)(18 m/s)=180 Ns$

I don’t think it’s unreasonable to assume that there was minimal friction between the car roof and the surfboard, such that it left the car going 40 mph. Since its mass didn’t change, its momentum after the collision is (surprise, surprise):

$p_{2}=mv_{2}=(10 kg)(18 m/s)=180 Ns$

The car doesn’t transfer any of its momentum to the surfboard. The surfboard simply retains its original momentum, which makes sense when you consider a less frequently cited definition of force as the time rate of change of momentum:

$\vec{F}=\frac{d\vec{p}}{dt}$

There are no forces acting on the surfboard during the collision (though there are LOTS of forces acting on the car), so it’s momentum is unchanged. The only reason you’d want the car to be stopped pretty fast is that there is a little friction between the surfboard and the car roof, and you don’t want it to last very long. Think about pulling a table cloth out from under some dishes. If you do it fast enough, it has a minimal effect on the dishes (surfboard).

When they take their board to NASA for the water tunnel experiments, we have the opportunity to think about some more sophisticated concepts. For something passive like a paper airplane (or a surfboard) to fly “stably”, any perturbations from its preferred orientation must induce forces that will correct itself and restore the original orientation. That is, as the surfboard began to pitch down, there would be a pitching moment created that would prevent it from nose-diving into the concrete.

If you ever played with paper airplanes, maybe you used paper clips to change the location of the center of mass so that your paper airplane was more stable. Without the center of mass in the correct place, your poorly designed paper airplane would veer off course. The surfboard in this case is like a poorly designed paper plane. The team observed with Kari’s surfboard that it would pivot wildly in NASA’s water tunnel. A stable surfboard would have maintained its orientation to the flow even if it were nudged up or down.

I’m not really sure what they try to accomplish with the 3D-printed surfboard. Instead of letting it pivot, they clamped it at the back so that it wouldn’t move… which kind of defeats the purpose. Of course it’s a streamlined body, so it’s going to have a quiet signature, but I don’t see how that is informative when it come to the matter of stable flight. I’ll cut Kurt Long some slack since I’m sure the many hour conversation was edited quite heavily.

Rayleigh Benard Convection

January 16th, 2011 No Comments

I know that this is probably pretty common to see, but I try to avoid heating up vegetable oil regularly. That being said, I had occassion to heat up a thin layer of cooking oil while preparing dinner yesterday and noticed a geometric pattern take shape in the surface of the oil.

I knew enough about what I was looking at to know that I should know what I was looking at. A quick internet search revealed that these hexagonal cells are manifestations of Rayleigh Benard convection. Basically, as long as the temperature gradient isn’t too big (I snapped this pick while the stove was heating up), these tidy little convection cells order themselves in a honeycomb pattern of circulating fluid, dissipating heat at the surface.

It’s amazing the science you can see all around you if you’re paying attention!

Optimum College Field Goal Distance

January 15th, 2011 No Comments

Dr. Allain wrote up a great post on this subject, so I’ll reduce the scope of what I was going to say, and let you read his analysis for the rest of the story. He used dot products for a much more elegant analysis than my trig-based approach.

I’ll focus on a more specific question pertaining to college football. With the has marks so much wider than the actual field goal posts, the angle that the kicker must aim for can be quite severe, especially close to the posts. My question is, is there a distance where it would behoove the kicker to kick from farther away (I don’t mean in order to move it more to the center of the field, I mean straight back)? Instead of snapping the ball 7 yards back from the line of scrimmage, maybe snap it back 10 or 12 yards. At the extreme hash, what is the optimum distance from which to kick to give yourself the best opportunity to make the field goal?

For our purposes, we will consider this a 2-D problem, where the height of the goal posts don’t matter. The kicker’s ability to make a field goal only depends on his aim. The wider the acceptable angle envelope ( $\alpha$ ), the better the chances of making the kick.

In our diagram, let’s define $\theta=\alpha+\beta$ . It is easiest to calculate $\alpha$ as $\theta-\beta$ since $\theta$ and $\beta$ are easy to calculate as arctan’s:

$\alpha=\theta-\beta=tan^{-1}\frac{w_h + w_p}{2d}-tan^{-1}\frac{w_h - w_p}{2d}$

To calculate the maximum value of alpha, we just take the derivative with respect to the field goal distance, $d$ . It’s a little hairy; I had to look up the derivative of arctan, do some variable substituting, but it beats integration. I ended up with,

$\frac{d\alpha}{dd}=\frac{d\theta}{dd}-\frac{d\beta}{dd}$
$\frac{d\alpha}{dd}=\frac{-w_h-w_p}{4d^2+w_h^2+2w_pw_h+w_p^2}-\frac{-w_h+w_p}{4d^2+w_h^2-2w_pw_h+w_p^2}$

which can be solved for $l$ after setting $\frac{d\alpha}{dd}$ to zero:

$l=\sqrt{\frac{2w_h^2-w_p^2}{8}}=\sqrt{\frac{2(40 ft)^2-(18.5 ft)^2}{8}}=18.9 ft$

So the angle $\alpha$ is maximized at $l=18.9 ft$ . Good, but unexciting result. That It means that it only makes sense to move straight back when kicking inside of 18.9 ft (~6.3 yards). That’s inside the end-zone. So forget I said anything… At least I don’t have to wonder anymore.

Storm Chasing Myths

October 13th, 2010 2 Comments

I’m getting beaten by the surface of this thing. Like being spanked.
Jamie Hyneman

So let me open by making a snide remark: I have never seen the boys so anxious to hand out “Confirmed” placards as they were in this episode. Call me a cynic, but I’m not sure they were as unforgiving in this episode as normal. Case in point: nothing got properly busted up.

For instance, they laid out some requirements for the personal protection shield, such as the need to be resilient against changing wind directions and resistance to debris. These both seem like reasonable requirements, and yet, they weren’t applied to the Storm Chasers cars… Haven’t we already learned that the most dangerous part of a hurricane/tornado is not the wind itself, but flying debris? Would it have killed them to shoot a wood block (or better yet, some substantial pieces of metal) at the trucks’ windows? I mean, until you’ve tested those things against some serious debris, calling them tornado-proof really seems like wishful thinking. And while I believe fending off debris would be their biggest problem, I’m not sure that the TIV-2 (the one with the spikes) would have much luck if the winds flipped 180 degrees. While the Dominator was more or less sheltered from wind in all directions (as demonstrated when it rotated 90 degrees and skid along the ground), the TIV-2’s backside did not look the least bit aerodynamic.

I liked Jamie’s solution for a personal protection system, and while they subjected it to more tests than they did the cars, I’m not sure it deserved as much praise as it got. For instance, they are baselining its performance with seeing what Adam withstood while standing. And they actually have the gall to call this the “control”. Generally, when you perform a control, you’d like to keep as many other things the same as possible. So why was Adam standing instead of laying in the prone position? You’re guess is as good as mine. They ended up comparing apples to oranges, when talking about the performance enhancement of the personal protection shield.

Last but not least, I wish someone pointed out that Jamie’s little fin at the back was worse than useless. All it did was spank him, apparently. I’m not saying that if the wind direction changed, the pod wouldn’t/couldn’t move to face the new oncoming direction, but I will say the fin would not have helped in that endeavor. Might as well not be included.

In conclusion, for the second time in two new episodes of fall 2010, I have very little math/physics to sink my teeth in. Let’s hope future new episodes have more quantitative content to think about and analyze.

Unarmed and Unharmed

October 9th, 2010 No Comments

Shoot this puppy.
Adam Savage

I love taking quotes out of context. Only for comedy. Never to win an election.

In this Buster’s Cut, the Mythbusters get pretty ambitious with physics and math. Grant even fills up a whole bus-side full of equations! Although the most impressive part of the whole episode was Adam’s freehand full-size cowboy drawing. But was there substance to their style?

De-Gunning

Jamie and Adam test the old Western cliche of the good guy being able to shoot the gun out of the bad guy’s hand leaving him “unarmed and unharmed”. They make it pretty clear that ubiquitous shrapnel will prevent the “unharmed” bit of the myth from being fulfilled. The “unarmed” part, however, is open for debate.

The fellas saw that they could shoot a gun out of their very unscientific metal band/Velcro hand. But what is a (surprised) human really capable of? They test this a couple different ways.

Swing Away

Adam pops out a nice little aluminum Wile E. Coyote looking gun that he lets Jaime smack with a bat. I assume they didn’t just make up the following numbers; he said that the gun was hit with a 800 gram bat swinging at 85 mph (38 m/s). This sounds pretty fast; they don’t specify, but for simplicity, we’ll say that it was the center of mass that that hit the gun with that speed (in fact, I guarantee the situation was far more complicated). Additionally, apparently their bullets are 15 g traveling at 613 mph (274 m/s). Okay, I’m following so far. Then they say they have comparable potential energies (428 vs. 416 ft-lb).

Excuse me?

Let’s assume that everyone on the show had a brain fart, and they meant kinetic energy. Which if it’s transferred quickly enough, has the potentialto knock a gun out of someone’s hand. So let’s calculate it ourselves:

Bat: $\frac{1}{2} mV^{2}=\frac{1}{2}(0.8\mbox{ kg})(38\mbox{ m/s})^{2}=578\mbox{ J}=426\mbox{ ft-lbf}$
Bullet: $\frac{1}{2} mV^{2}=\frac{1}{2}(0.015\mbox{ kg})(274\mbox{ m/s})^{2}=563\mbox{ J}=415\mbox{ ft-lbf}$

Great! Those check out amazingly well with the show. Now here’s the rub. Both of those are reported as simply energy. From the standpoint of hold-on-ability, it’s not the energy nearly as much as it is the power (rate of energy transfer). Kinetic energy isn’t even the right thing to look at here. It is plain from the high speed that pieces of the bullet are speeding away after they break on the gun, carrying kinetic energy away that’s not left with the gun.

In fact, they make the classic mistake of interchanging units, and the narrator actual says that the two scenarios resulted in equal forces. What’s really important here, is the momentum that’s transferred, because a square hit is going to make sure the bullet surrenders all of its forward momentum (let’s pretend it doesn’t rebound backwards, but it can rebound sideways), and we never forget, momentum is always conserved. Compare the momentum of the two objects:

Bat: $mV=(0.8\mbox{ kg})(38\mbox{ m/s})=30\mbox{ kg m/s}$
Bullet: $mV=(0.015\mbox{ kg})(274\mbox{ m/s})=4\mbox{ kg m/s}$

Um, no wonder the bat felt worse that the bullet. This is where the concept of impulse comes into play. It is simply the change of momentum: $I=\Delta p=mv_{2}-mv_{1}$

Of course, if you’d like to get calculus involved (and why wouldn’t you?), you can also write impulse as:

$I=\int_{t_{1}}^{t_{2}}F\:dt$

In other words, how long it takes for momentum to transfer is nearly as important as the quantity of momentum. If the force is constant in time, the equation simplifies to $\Delta p=F\Delta t$ . So if the bullet applies a constant force over a very short time, it will take a very large force to balance the equation. The shorter the time, the larger the force. They intuitively knew this after their test with the string to pull the gun out of Jaimie’s hand, which they deemed did not have enough “sting”. Basically, the momentum transfer was smeared out as too small a force over too long a time.

Newton’s Law

The concept of impulse dovetails nicely into my last little commentary about the gun-slinging. Jaime builds a nifty little device to test the actual force felt when a gun in his hand is shot (because they are rightly suspicious of their bat demonstration). It simply adds a handle that allows him to hold a gun at an such that the barrel is point in the direction from whence a bullet may come.

Jaimie claims that Newton’s 3rd law says it will produce an equivalent force as if the gun was shot at with a bullet. Well, yes and no.

Yes, Newton’s 3rd law is something along the lines of for every action, there’s an equal and opposite reaction. In fact, for clarity, let’s just say for every force, there’s an equal and opposite force.

No, Newton’s 3rd law does not say the force will be the same as having your gun shot at.

Why? The answer still lies with the time over which momentum is transferred. They will experience the same change in momentum, but that change will manifest itself as different forces being applied over different times (remember $\Delta p=F\Delta t$ ?). The whole point of having a barrel is that a smaller force can be applied over a longer distance, preserving the integrity of the bullet. This exactly the opposite of bullet impact, where the bullet is slowed down in a fraction of the time, resulting in the bullet’s dismemberment.

With all that being said, in both cases, the momentum is probably delivered so quickly that a shooter wouldn’t feel the difference (all of the momentum would be transferred before the hand can react). So it may seem I am quibbling (and I am), but their justification for what they did was shaky, at best.

Superhero Hour

October 3rd, 2010 No Comments

We’re going to select our cable to be more than adequate to handle that amount of force
Grant Imahara

This 2007 episode saw the Mythbusters scale tall buildings, change in phone booths, and bust themselves in the nose. It also involved an attempt to turn a car (based on a Batmobile) around a tight turn using a cable launched at a pivot point.

Grant used some (emphasis on some) physics to help figure out what sort of cable they’d need. To figure out the tension in the cable, Grant turned to centripetal force/acceleration.

Centripetal acceleration is $\frac{V^{2}}{R}$ , so of course, the centripetal force would come out to $\frac{m V^{2}}{R}$ . Just as Grant said, it’s a function of the car’s mass, speed, and the turn radius. Let’s try to figure out how/why Grant predicted they would need 7000 lbs of force. I’m going to guess that they were making the turn with a 15 foot (~ 5 meter) radius. We know the speed was 30 mph (13 m/s), and I’ll guess that the car’s mass was 2000 lbs (900 kg). A little algebra later:

$\frac{m V^{2}}{R} = \frac{(900\: kg)(13\: m/s)^{2}}{5\: m} = 30,000 \: N = 6700 \: lbs$

Hey, that’s pretty close to 7000 lbs! Not bad. I promise, those were my first guesses. Okay, so why did it break then? Well, there are a couple of things I can think of.

The cables they used may be able to support 7000 lbs when applied gradually along an unmolested run of rope. The reality of the situation is much harsher. For one, the cable wrapped around the steel structure is kinked where it presses against the edge, compromising strength and intensifying the stress. Furthermore, generally when something is loaded very quickly, it appears to behave weaker than it otherwise would. This is because when an object experiences impact loading, it doesn’t have the ability to dissipate energy as efficiently as it would in a more gradual loading situation. Of course, that can hardly be avoided in this case.

Maybe Batman used a spider web cable. Or nanotubes. Nanotubes can do anything.

Space elevator?

No problem.