Ready for the Naked Avenger!
Tori Bellacci

I was pretty excited that both pieces of this episode actually involved some physics, as opposed to the regrettable (on so many levels) Battle of the Sexes episode.  However, I knew I would have to go to work on this post as soon as Jamie and Adam started equating speed and energy.

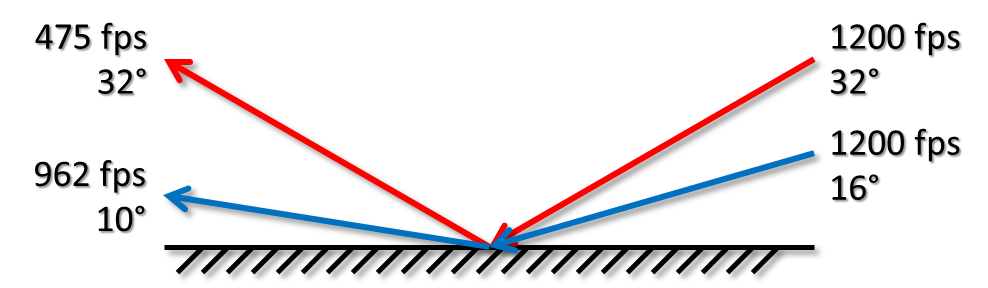
They were interested in how a bullet ricochets off of asphalt when fired at different angles.  At a shallow firing angle (16 degrees), they noted that the velocity decreased from 1200 fps to 962 fps.  This is not a huge decrease in speed, but knowing that energy is proportional to the square of velocity, I was not willing to say that it was “not a lot of loss”.  In fact, for a bullet mass , we can calculate the two energies, before and after impact (note that when you multiple by mass, you get units of energy):

In other words, the energy decreases to 64% of the original value (less than the 75% that Adam later quoted).  Losing more than a third of the energy doesn’t seem like something so easily dismissed.  So I was suspicious our heroes were confusing momentum with energy, and forgetting to square the velocity.

The misconception was cemented by Adam when they moved on to the steeper shot at 32 degrees.  In that case, the velocity dropped from 1200 to 475 fps.  Adam said that this had “lost almost two-thirds of its energy”, but now we know better:

It lost 84% of it’s energy!  Quite a bit of energy to give up during a ricochet!

So while it might seem like nit-picking (and to an extent, it is), there is really an important point here that energy is not linearly related to velocity but to the square of velocity.  This is a concept that is important to keep in mind; energies tend to fluctuate greatly as velocities change, and large velocities result in very large energies.

I just wanted to chime in on the other myth of the blast-aided jump.  I thought they did a pretty good job with this; the nitrogen gun was impressively consistent and the high-speed video was fantastic.  They barely touched on this concept of pressure versus impulse, but going to the anfo was definitely a step in that direction.

Anywho, pressure waves have two important components.  One is the increase from atmospheric pressure, and the other is the duration.  The time integral of the over the duration of the blast (times the area of the target) is called the impulse.  While a large  can do damage to a human body, essentially jostling adjacent cells apart from each other, in order to really do damage to object and throw things around, you need a big impulse, delivered, which means the pressure and time need to conspire to impart a lot of momentum.  Hence the slow exploding anfo.

I admit, I was also disappointed, if not surprised, that Buster didn’t get pushed a whole lot.  They sort of addressed my concern about a small exposed area (over which to integrate said ) by attaching their bed-liner sail.  I guess I’ll just go watch The Avengers to satiate my appetite for unrealistic explosions.